WRIGHT BROTHERS WIND TUNNEL

Inventors improve the quality of life the world over.

Once in a while a significant scientific advance may go unnoticed because there are greater, more exciting things afoot. Such is the case of the Wright brother's wind tunnel and the fundamental research they did in aerodynamics in the winter of 1901-1902. The Wright wind tunnel experiments resulted in a breakthrough without which the airplane might never have gotten of the ground. But what Orville and Wilbur did next - invent an aerodynamic control system, make the first controlled powered flights, and develop a practical airplane - completely overshadowed their wind tunnel work.

 

As a result, biographers of the Wright brothers tend to breeze past the wind tunnel on their way to the exciting stuff just a little further down the timeline. They dutifully relate the necessary facts, telling us the wind tunnel and its balances were deceptively crude. The tunnel was little more than a pine box and the balances were fashioned from worn out hacksaw blades and discarded bicycle spokes. Yet the data gleaned from the tests was remarkably accurate, despite the homespun appearance of the instruments. The Wright wind tunnel experiments marked the first time that anyone had measured the lift and drag produced by various wing shapes with sufficient accuracy for them to be of any use in aircraft design. And with that, the biographers leave the Wright's laboratory work and get back to the flying.

 

 

 

Replica of Wright Brothers' Wind Tunnel

 

 

Enthusiasts to Amateur Scientists

 

This is unfortunate because the wind tunnel experiments are the stuff that world-class aviation history is made of. The Wrights drew back the curtain on the elusive laws of physics that allow us to fly and exposed them in neat rows of numbers. And more important than the numbers themselves are what measurements the brothers chose to make.  

 

Wright biographers completely miss the wind tunnel story when they tell us that the Wrights were the first to make accurate measurements. Several investigators prior to Wilbur and Orville had conducted experiments with wing shapes that produced reasonably good numbers. But these earlier pioneers had an incomplete understanding of the dynamics of a wing in flight.

 

Consequently, the forces they chose to measure or how they interpreted their data rendered their efforts less useful than they might have been. Furthermore, no one before Wilbur and Orville checked their data against the performance of an aircraft in flight. The Wrights were the first to verify laboratory results with actual flight tests. If they had never done anything beyond compiling and verifying their lift and drag tables, we would still remember the Wright brothers for their substantive contribution to the development of aviation.

 

The wind tunnel also marked an important change in the intellectual posture of the Wright brothers. Prior to September 1901, they were more enthusiasts than scientists. They were well read in aeronautical science, but naïve in its application. The biographers tell you that the Wrights used Otto Lilienthal's lift tables to design their first two gliders. Lilienthal was the world's first successful glider pilot, having designed and flown his own gliders between 1891 and 1896. He used a whirling arm apparatus to measure the forces on a wing. The Wrights began to suspect that Lilenthal was wrong when their gliders failed to develop the predicted lift. What the biographers miss is that the Wrights applied these tables incorrectly, using lift data for Lilienthal's wings to predict the performance of their own wing designs, even though the shapes differed markedly.

 

That being so, it's not surprising that the performance of the Wright's early gliders was disappointing. The brothers first attempted to fly in 1900, making a pilgrimage to the sand dunes near Kitty Hawk, North Carolina where the winds were stronger and the ground softer than in their hometown of Dayton, Ohio. They brought with them a biplane glider with a wingspan of 17-1/2 feet and a parabolic camber of 1/20. They had designed this glider interpolating Lilienthal's data for his standard arc-shaped 1/12 cambers. When the 1900 glider failed to produce the expected lift, the brothers increased the wingspan of their 1901 glider to 22 feet and the camber to 1/12, but retained the parabolic shape. They also increased the chord to make wide wings, unaware that a low aspect ratio - the ratio of wingspan (length) to chord (width)  - can also reduce lift and cause control problems. As a result the 1901 glider performed worse than the 1900 in many respects. The brothers rigged the glider with a complex system of wires and ropes that reduced the camber to 1/19. This salvaged the 1901 flying season, allowing them to make a few manned flights. But the glider's performance was not what they had hoped. Wilbur was so dejected during the train ride back home that he commented that he did not believe that man would fly in their lifetimes, possibly not for another thousand years.

 

 

 

Wright Brothers' - Calibrated lift balance

 

 

In fact, Wilbur and Orville came very close to abandoning their aeronautical ambitions. But waiting for Wilbur when he arrived home in Dayton, Ohio was an invitation from Octave Chanute to come to Chicago to speak to the Western Society of Engineers about their gliding experiments. Chanute was a highly respected civil engineer, an aeronautical visionary, and a prolific correspondent with many experimenters in the aviation field. Wilbur was flattered by Chanute's invitation, but it presented a quandary. Neither Wilbur nor Orville considered that their experiments to date were worth the attention of such a learned body, even though they had been able to make about 40 respectable glides on their 1901 glider. However, they had done one thing that might be of interest to these engineers. They were the first aeronautical investigators ever to measure the performance of their aircraft in actual flight and compare the results with laboratory data -- in this case, Lilienthal's data. Their quandary was that the flight performance did not match the data and they had absolutely no idea how to explain this discrepancy except a hunch that Lilienthal's tables were wrong.

 

Wilbur decided to say as much in his speech. We don't know exactly what he said -- he rewrote the speech for publication after he was well along with his wind tunnel experiments and is reported to have softened the things he said about Lilienthal's work. He may have also changed other sections since his understanding of aerodynamics matured quickly after his speech. But whatever he did say, it stirred up a good deal of interest. Chanute reported to Wilbur that there were many requests for copies of his speech.

 

It seemed to stir something in Wilbur and Orville, too. Just before Wilbur left to deliver his speech, he and Orville experimented with a crude wind tunnel made from a soapbox. The experiments seemed to satisfy them that Lilienthal's tables were indeed wrong and Wilbur was safe in saying so to the Western Society of Engineers. When Wilbur returned from giving the speech, the brothers devised another experiment. They mounted a wheel horizontally on a bicycle, then attached a flat plate and a miniature wing or airfoil to the wheel. These were positioned so that when the bicycle was pedaled fast enough to create a wind blowing over the wheel, the drag on the plate was balanced against the lift generated by the wing. This too indicated that there were problems with Lilienthal's tables, but the apparatus was imprecise. In order to get the data they needed to build flying machines, they would have to devise a precision instrument. 

 

They decided to build a wind tunnel and balances.  Once the Wrights determined to collect their own lift and drag information, there was a phenomenal change in the brothers over the span of a few months. They quickly put their inexperience behind them and carefully thought through the aerodynamic forces on a wing in flight, defining in their own minds what they should measure. Once they had made these measurements, they learned to apply their new data properly to aircraft design and came to a better understanding of the relationship between lift, drag, and wing shapes than anyone else in their field. In September 1901, they were part-time investigators, badly discouraged by their failures and hamstrung by their lack of experience and understanding. By January of 1902, they were creative and confident scientists pushing back the frontiers of aeronautics.

 

 

---

 

 

My brother Orville and I built a rectangle-shaped open-ended wind tunnel out of a wooden box. It was 16 inches wide by 16 inches tall by 6 feet long. Inside of it we placed an aerodynamic measuring device made from an old hacksaw blade and bicycle-spoke wire. We directed the air current from an old fan in the back shop room into the opening of the wooden box. In fact, we sometimes referred to one of the two open ends of the wind tunnel as the "goesinta" and the other end as the "goesouta." An old one-cylinder gasoline engine (that also turned other tools in the shop, such as our lathe) supplied the power to turn the fan. This was because there was no electricity in our shop. In fact, even the lights were gas lights.

 

It took us about a month of experimenting with the wind tunnel we had built to learn how to use it effectively. Eventually we learned how to operate it so that it gave us results that varied less than one-tenth of a degree. Occasionally I had to yell at my brother to keep him from moving even just a little in the room because it would disturb the air flow and destroy the accuracy of the test.

 

Over a two month period we tested more than two hundred models of different types of wings. All of the models were three to nine inches long. Altogether we measured monoplane wing designs (airplanes with one wing), biplanes, triplanes and even an aircraft design with one wing behind the other like Professor Langley proposed. Professor Langley was the director of the Smithsonian Museum at the time and also trying to invent the first airplane. On each little aircraft wing design we tested we located the center of pressure and made measurements for lift and drift. 

 

We also measured the lift produced by wings of different "aspect ratios." An aspect ratio is the ratio or comparison of how long a wing is left to right (the wing span) compared to the length from the front to the back of the wing (the wing chord). Sometimes we got results that were just hard to believe, especially when compared to the earlier aerodynamic lift numbers supplied by the German Lillienthal. His numbers were being used by most of the early aviation inventors and they proved to be full of errors. Lillienthal didn't use a wind tunnel like Orville and I did to obtain and test our data.

 

We finally stopped our wind tunnel experiments just before Christmas, 1901. We really concluded them rather reluctantly because we had a bicycle business to run and a lot of work to do for that as well.

 

It is difficult to underestimate the value of that very laborious work we did over that homemade wind tunnel. It was, in fact, the first wind tunnel in which small models of wings were tested and their lifting properties accurately noted. From all the data that Orville and I accumulated into tables, an accurate and reliable wing could finally be built. Even modern wind tunnel data with the most sophisticated equipment varies comparatively little from what we first discovered. In fact, the accurate wind tunnel data we developed was so important, it is doubtful if anyone would have ever developed a flyable wing without first developing this data. Sometimes the non-glamorous lab work is absolutely crucial to the success of a project.

 

In any case, as famous as we became for our "Flyer" and its system of control, it all would never have happened if we had not developed our own wind tunnel and derived our own correct aerodynamic data.

- Wilbur Wright

 

 

 

---

 

 

The Wright brothers tested over 200 airfoils and prepared complete tables for about four dozen. But there was one more step to take before they had all the numbers they needed to design an aircraft.

 

 

 

The wind tunnel has a scoop with two sets
of vanes to provide a smooth air flow.

 

The wind tunnel had been invented in England in 1871by Francis Wenham and John Browning, who used it to study both wing camber and aspect ratio. Over the next three decades, several other experimenters used it for aeronautical research, mostly in Europe. The 1901 Wright wind tunnel was the second or the third in America.

It's telling that the Wright brothers built their wind tunnel and balances and began collecting data before they had a clear understanding of aerodynamic forces or the measurements they wanted to make. Prior to the January 1902, the terms that Wilbur uses to describe aeronautical forces aren't clearly defined in his mind, and he makes conflicting statements. In all fairness to Wilbur, this is not just a measure of his initial confusion but also the confusion that existed in the field at the time. The components of lift and drag were hotly debated, terms had various meanings depending on how they were used and who was using them. But it's also a good example of how the Wright brothers best worked through a problem. They were "hands on" investigators. To figure out what they were going to measure, they started making measurements.

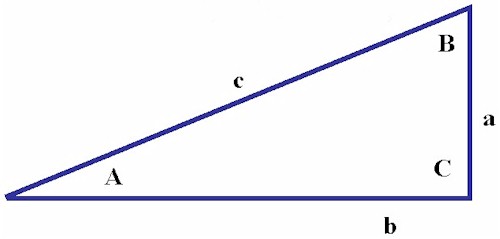
If you are unfamiliar with trigonometry, here's a quick primer. "Trig" depends on ratios called sines, cosines, and tangents - one side of a right angle triangle divided by another. For a triangle with sides a, b, and c and angles A, B, and C as shown, the ratios are as follows:-

Right angle triangle

These ratios are different for each angle but remain constant with size -as long as the angles between the sides remain the same, the ratios are unchanged same no matter what the size of the triangle. Consequently, if you know the magnitude of just one side and one angle (other than the right angle), you can calculate the other two sides by looking up the sine, cosine, and tangent ratios of the known angle and multiplying the appropriate ratio times the known side.

"Normal" was used in the Wright's day much the same way we use "perpendicular" today. The normal force was lift perpendicular to the wing chord. True lift was parallel to the force of gravity and perpendicular to the horizon. Because the wing usually flew at an angle of incidence (our modern angle of attack) that was not parallel to the horizon, the normal force was often at an angle to true lift and the force of gravity. When added up, the forces on the wing resolved themselves into the resultant pressure. Many aeronautical investigators considered that this pressure must correspond with true lift, but Wilbur thought it must be angled slightly forward of lift to compensate for head resistance -- what we now call parasitic drag. The tangential was calculated from the angle between the resultant pressure and the normal force by multiplying the tangent times the normal force:

When the angle of incidence was positive (the normal was behind the resultant pressure), the tangential was considered to retard the forward motion of the aircraft and it was added to the drift (drag) to arrive at total resistance. When the angle of incidence was negative (the normal was ahead of of the resultant pressure), the tangential was part of the force that propelled the aircraft and it was subtracted from the drift. Thinking this through, Wilbur added another wrinkle. On any given wing shape, lift did not begin when the chord was parallel to the wind -- it began when the wing was positioned at a slightly negative angle of incidence (attack). This was the zero of lift. Wilbur suggested that the true normal be calculated from the zero of lift rather than the chord. He also suggested that the true tangential should be calculated from the angle between the resultant pressure and the true normal. But after he had finally gotten his mind around all these confusing concepts, Wilbur seemed to see them for what they were -- overthinking the problem. Much of his brilliance was his ability to simplify. Wilbur declared lift and drag to be the keys to aeronautical design and went with his convictions. History has shown that it was a good call -- modern aeronautics has nothing like the tangential.

In the Wilbur and Orville's time, aeronautical investigators studied two distinct types of flight -- soaring flight and dynamic flight (what we now refer to as gliding flight and powered flight). Scientists considered both types to be similar, but the forces in play and the mathematics used to analyze them were somewhat different. Wilbur and Orville were squarely in the soaring camp in 1901. In fact, there is no real evidence to suggest that they planned to attempt dynamic flight at this time, although Wilbur sometimes discussed its theory with Chanute. But they never performed a single experiment that had a direct application to dynamic flight until late October 1902. Their 1901 wind tunnel tests, the forces they measured, and the tables they compiled were all designed to solve problems in soaring flight. One example of this is the importance they placed in the lift/drag ratio. This number was central to the performance of a glider -- the higher the ratio (more lift, less drag), the better the gliding angle irregardless of the weight of the glider and its pilot. The Wrights were perhaps the first to understand this.

Initially, the brothers cut the plate into five fingers. But when they mounted the fingers on the balance, they found one of the fingers near the frame was affected by eddies in the wind coming off the frame. They removed this finger, cut it in two and soldered the parts to two of the remaining fingers. This accounts for the seemingly random length of the fingers. In their final tests, the Wrights used some air foils with 8 square inches of surface area -- a third more than the drag fingers. To compensate, they added another third of the sine of  to find the coefficient of lift:

Each balance had two pointers, but just one was used to indicate the angle on the scale. The second pointer balanced the force of the wind hitting the first pointer and kept it from affecting the measurement.

Wright Brothers' - Wind Tunnel propeller

Wilbur's original estimate of the wind speed in the tunnel was 40 feet per second, or about 27 miles per hour. Later, his estimate was revised downward to 25 miles per hour. This velocity would have been very difficult to achieve given the equipment the Wrights were using. When we reproduced the wind tunnel and duplicated the experiments, we used a four-bladed balanced fan running within 10 percent of its maximum safe speed. This produced airflow in the tunnel of 20.3 miles per hour. The Wrights were using a homemade fan with just two blades. It was not dynamically balanced and could not have run for long periods of time at speeds in excess of ours without flying apart. Even if it held together, the vibration at high speeds would have interfered with the experiments. While he was engaged in the wind tunnel tests, Wilbur commented to Octave Chanute that the Richards anemometer they had used at Kitty Hawk (and probably used for the wind tunnel tests) recorded high. Taking all this into account, it's likely that the wind blowing through the Wright's tunnel was less that 20 mph.

The Wrights called this their "tangential measuring machine." Because they rotated the entire balance, including the scale, the pointer indicated an angle that expressed the ratio of lift to drift minus the angle of incidence (attack). This was essentially the angle used to calculate Lilienthal's tangential force. To get the ratio of true lift to true drift, they had to add the angle of incidence to the angle indicated on the pointer. They sometimes called this the gliding angle, not to be confused with the modern definition of the term, which describes the angle at which a glider descends through the relative wind.

There is no written record that the Wright brothers actually made these calculations to establish the value of the coefficient of pressure. Wilbur had already written Chanute that he suspected the answer was .0033; this was the number that best explained the lift and drag he and Orville had measured when flying their 1901 glider at Kitty Hawk. But with the wind tunnel experiments, the Wright brothers had developed into world-class scientists. It's inconceivable that they wouldn't have taken this final step to confirm their hunch.

The reasoned approach the Wright Brothers took to solving the problem of flight and the diligence with which they pursued their goal is not generally appreciated. The science of aerodynamics, the physics as described by mathematical equations, had been codified centuries earlier by men such as Newton, Bernoulli, Euler, Navier, and Stokes; men who's names are attached to some of the fundamental equations of fluid dynamics. However, not until the Wright Brothers had anyone successfully conquered the engineering - turning the science into an airplane of practical use. Beginning in 1899, Wilbur and Orville executed a research and development program that resulted in not just the 1903 Flyer, but in the first truly practical heavier-than-air flying machine in 1905.

The Wrights gained a thorough appreciation of the state of the art (alluded to above in reference to the work of Lillienthal and Langley) through correspondence with some of the well known aviation researchers of their day and from the writings of others, and used this knowledge as a starting point for their own work. However, the Wrights were not blinded by reputation; when the results of their own experiments did not match the predictions based upon existing theory and published data, the two brothers devised means to obtain the data they required via experiments with full-scale kites, both manned and un-manned, and with sub-scale models tested in a wind tunnel of their own design.

With respect to the wind tunnel, it is interesting to re-read the fifth paragraph above. Wilbur does not claim to have invented the first wind tunnel, Edme Mariotte published a description of a wind tunnel in "Traite du mouvement des eaux" in 1686, and Wenham and Browning constructed one in the 1870's. Rather, theirs was the first tunnel where accurate sub-scale aerodynamic data was obtained and systematically recorded for later application to the design of the full-scale Flyer. To this day the process is essentially the same - engineers first design according to theory then test their designs sub-scale in the wind tunnel. Yet there is one significant difference between modern day wind tunnel tests and the Wright Brothers work. The Wrights relied primarily on parametric data of components, while most modern wind tunnel tests are conducted on models which are as accurate a representation of the aircraft design as limitations of the tunnel and of the model size permit.

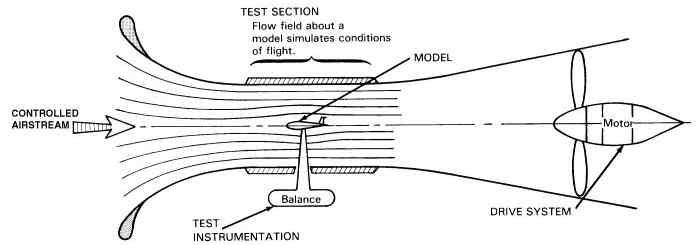
Wind Tunnel basics

The heart of the wind tunnel is the test section where a scale model is supported in a carefully controlled airstream that produces a flow of air about the model that duplicates the full-scale aircraft. Appropriate balances and test instrumentation measure the aerodynamic characteristics of the model and the field around it (its flow field). Although the form of a wind tunnel can vary, all wind tunnels have a drive system, a test section, use a model that is supported in an airstream and whose characteristics are measured by test instrumentation. The wind tunnel allows the aerodynamic forces of lift, drag, and side force in reference to the tunnel axis (the axial centerline of the test section) to be measured.

The Wright brothers used two simple instruments to measure the lift and drag of their airplanes in flight. The spring scale gave them the magnitude the hypotenuse of the lift-drag triangle in pounds. The clinometer provide the angle of the hypotenuse as measured from the lift side. With these two numbers and a little trigonometry, they were able to calculate the lift and drag.

Spring Balance and Clinometer

In a letter dated October 24, 1901, Wilbur explained to Octave Chanute how the lift balance he and Orville had designed would work. Wilbur’s diagram of the lift balance shows the lower arms of the balance, whereas the upper arms and the air foil are left to your imagination: "The arms ac bear the crosspiece aa and with the imaginary line cc form a parallelogram with the corners cc fixed and the arms ac turning on these points. The wind strikes the [drag fingers] (indicated by the short black lines) at an angle of 90 degrees in all positions of arms ac. Now if the lift [generated by an air foil on the upper arms is] transmitted to the point a and applied at right angles to arms ac, the [drag fingers] will [move] to the position indicated by the dotted lines and the pressure exerted will be as ax is to ay, i.e. the lift will be equal to the sine of the angle aca."

Replica of Wright Brothers' - Lift Balance

FINDING THE RIGHT FORMULA

To understand the difficulty of the problem the Wrights faced in September 1901 and the genius it took to solve it, you need to understand the mathematics behind the pine box and the used hacksaw blades that made up the tunnel and balances. If you are one of the mathematically challenged, don't despair - the logic behind the formulae is easy to grasp. In fact, you may have an advantage over someone educated in aeronautics. The methods used to analyze lift and drag today are different from what the Wright brothers used. Modern aeronautics looks at the forces in play on a wing as vectors. The Wright brothers and their contemporaries thought in terms of angles. Today, we use a form of calculus called vector analysis to study these forces; the Wright brothers used simple trigonometry Because of this, contemporary aeronautical engineers often react by labeling these older methods as wrong or incomplete. In their historical context, however, they were the best methods available at the time.

This isn't to say that the Wright's analysis of lift and drag was simplistic. In a letter to Octave Chanute on January 5, 1902, Wilbur carefully defines the forces in play on a wing in flight, taking into account the angle of attack (which he refers to as the angle of incidence), the path of flight, and the wind relative to the motion of the aircraft. "It has been a problem for me, ever since we began our experiments...what pressures we should attempt to measure and what should be the basis of our table." He wisely decides to make those measurements that will be most useful to him in analyzing actual flights. "...true lift and true drift...are alone to be considered in calculating glides." True lift Wilbur defines as the pressure or force directly opposed to gravity and true drift is a force perpendicular to it - what we now call drag.

Lilienthal's tables, he notes, do not contain numbers that are immediately useful. Lilienthal based his table on the pressure perpendicular to the chord (the normal force) and the portion of that pressure that increases or retards the forward motion of the aircraft (the tangential force) Neither could be used directly to design an airplane. "...normal and tangential [must be reduced] into vertical and horizontal components, which is inconvenient and a waste of time," Wilbur wrote. It was a bold -- maybe even brash -- statement. Lilienthal's astounding success as a glider designer and pilot in the 1890s had made his scientific writings central to aeronautics. 

His emphasis on the tangential had led many investigators to conclude it was the key to soaring flight.But just five months after applying these tables incorrectly to the design of their 1901 glider, Wilbur now understands Lilienthal's tables and their limitations. The tangential, he knows, is a red herring. The Wright brothers will measure lift and drift. By doing so, they accomplished in a few months what had eluded other scientists for a century.

The brothers looked on these forces of lift and drift as the legs of a right triangle. This was the same triangle that Sir George Cayley drew in 1799 when he first conceived of the idea of a fixed-wing aircraft. Drift (or drag) was the base, lift was the side. According to the Pythagorean theorem that was drilled into most of us in high school, all the parts of that triangle -- base, side, hypotenuse, and the angles between them -- bear a distinct mathematical relationship to one another. By using simple trigonometry and ratios called sines, cosines, and tangents, the Wrights could find any part of the lift-drag triangle as long as they knew the magnitude of one part and one of the angles between the hypotenuse and another part.

They had used trigonometry to measure the performance of their glider when they flew them in Kitty Hawk. The brothers tied off the controls and flew each of the gliders as kites, attaching tether ropes to the leading outboard struts. The tether ropes, they noticed, stretched up at an angle. This angle was the result of lift and drag. The lower the lift or the higher the drag, the greater the angle of the rope as measured from the vertical. The rope was, in effect, the hypotenuse of the lift-drag triangle. Using an ordinary spring scale, they measured the tension on the ropes - this gave them a magnitude for the hypotenuse. They measured the angle  with a clinometer, a surveyor's instrument given to them by Chanute. This allowed them to reduce the tension on the tether ropes into the forces of lift and drag using a few simple trig formulas:

Once they had found these numbers for lift and drag, the Wright brothers plugged them into established formulae to determine whether their wings were developing the expected lift and drag. These lift and drag formulae had their beginnings in the work of John Smeaton, an English engineer that studied the action of water wheels and windmills. Smeaton observed that when the wind blew against a sail, energy was transferred in the form of pressure on the sail. The amount of pressure generated was proportional to the size of the sail and the velocity of the wind. Smeaton multiplied the surface area times the square of the wind velocity, then devised a multiplier to convert the result into pressure. This multiplier became known as the coefficient of pressure or "Smeaton's coefficient". Smeaton published this formula in 1759:

MASSACHUSETTS INSTITUTE OF TECHNOLOGY

MIT'S 'WRIGHT BROTHERS' WIND TUNNEL

INVENTORS A - Z

The ultimate Robot Boat. Solarnavigator uses an advanced SWASSH hull as the platform 

to mount the world's first autonomous circumnavigation. A successful expedition could pave the way for improved safety at sea.

This website is copyright © 1991- 2013 Electrick Publications. All rights reserved. The bird logo and names Solar Navigator and Blueplanet Ecostar are trademarks ™.  The Blueplanet vehicle configuration is registered ®.  All other trademarks hereby acknowledged and please note that this project should not be confused with the Australian: 'World Solar Challenge'™which is a superb road vehicle endurance race from Darwin to Adelaide.  Max Energy Limited is an educational charity working hard to promote world peace.

 AUTOMOTIVE  |  BLUEPLANET BE3  |  ELECTRIC CARS  |  ELECTRIC CYCLES  |  SOLAR CARS  |  SOLARNAVIGATOR