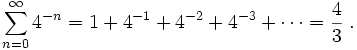ARCHIMEDES  287BC - 211BC

Inventors improve the quality of life the world over.

Archimedes was the eminent mathematician and excellent physicist of his time. He was born in Syracuse, on the island of Sicily in 287 B.C. At that time Sicily was a Greek land. Archimedes was the son of an astronomer. He studied at Alexandria in Egypt, and then returned to Syracuse. He early became an astronomer. He constructed a brass planisphere - a projection of the celestial sphere - that showed the revolution of the Sun, the Moon and the five known planets, and showed the nature of eclipses.

Archimedes stone bust

During a Roman siege of Syracuse in 213 Archimedes kept off the attacks of the Roman forces. There is a legend, that he used a gigantic mirror which focused the Sun's rays upon the Roman ships. When the Romans overcame the Syracusan defences, they ordered to bring Archimedes to Rome. Archimedes was 75 at that time. A Roman soldier was near Archimedes after the breach of the city's defence. Archimedes, probably tired after his work during the siege, was sitting on the ground, drawing mathematical figures in the dust. A soldier ordered him to surrender, but the great mathematician paid no attention to him. The problem was more important to him. Archimedes said, "Get away from my circles, you dog!" The soldier killed the world's greatest thinker.

His planisphere was taken to Rome and was described by Cicero, 150 years later.  Archimedes is generally regarded as the greatest mathematician and scientist of antiquity and one of the three greatest mathematicians of all time.

Discoveries and inventions

Archimedes became a popular figure as a result of his involvement in the defense of Syracuse against the Roman siege in the First and Second Punic Wars. He is reputed to have held the Romans at bay with war engines of his design; to have been able to move a full-size ship complete with crew and cargo by pulling a single rope; to have discovered the principles of density and buoyancy, also known as Archimedes' principle, while taking a bath (thereupon taking to the streets naked calling "eureka" - "I have found it!"); and to have invented the irrigation device known as Archimedes' screw. He has also been credited with the possible invention of the odometer during the First Punic War. One of his inventions used for military defense of Syracuse against the invading Romans was the claw of Archimedes.

In creativity and insight, he exceeded any other mathematician prior to the European renaissance. In a civilization with an awkward numeral system and a language in which "a myriad" (literally ten thousand) meant "infinity", he invented a positional numeral system and used it to write numbers up to 10⁶⁴. He devised a heuristic method based on statistics to do private calculation that we would classify today as integral calculus, but then presented rigorous geometric proofs for his results. To what extent he actually had a correct version of integral calculus is debatable. 

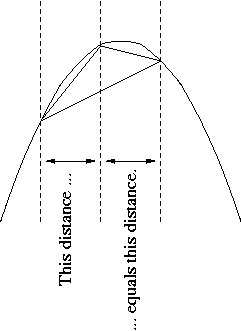
He proved that the ratio of a circle's perimeter to its diameter is the same as the ratio of the circle's area to the square of the radius. He did not call this ratio π but he gave a procedure to approximate it to arbitrary accuracy and gave an approximation of it as between 3 + 1/7 and 3 + 10/71. He was the first, and possibly the only, Greek mathematician to introduce mechanical curves (those traced by a moving point) as legitimate objects of study. He proved that the area enclosed by a parabola and a straight line is 4/3 the area of a triangle with equal base and height. (This proposition needs to be understood consistently with the illustration below. The "base" is any secant line, not necessarily orthogonal to the parabola's axis; "the same base" means the same "horizontal" component of the length of the base; "horizontal" means orthogonal to the axis. "Height" means the length of the segment parallel to the axis from the vertex to the base. The vertex must be so placed that the two horizontal distances mentioned in the illustration are equal.)

In the process he calculated the oldest known example of a geometric series with the ratio 1/4:

If the first term in this series is the area of the triangle in the illustration then the second is the sum of the areas of two triangles whose bases are the two smaller secant lines in the illustration. Essentially, this paragraph summarizes the proof. Archimedes also gave a quite different proof of nearly the same proposition by a method using infinitesimals.

He proved that the area and volume of the sphere are in the same ratio to the area and volume of a circumscribed straight cylinder, a result he was so proud of that he made it his epitaph.

Archimedes is probably also the first mathematical physicist on record, and the best before Galileo and Newton. He invented the field of statics, enunciated the law of the lever, the law of equilibrium of fluids and the law of buoyancy. (He famously discovered the latter when he was asked to determine whether a crown had been made of pure gold, or gold adulterated with silver; he realized that the rise in the water level when it was immersed would be equal to the volume of the crown, and the decrease in the weight of the crown would be in proportion; he could then compare those with the values of an equal weight of pure gold.) He was the first to identify the concept of center of gravity, and he found the centers of gravity of various geometric figures, assuming uniform density in their interiors, including triangles, paraboloids, and hemispheres. Using only ancient Greek geometry, he also gave the equilibrium positions of floating sections of paraboloids as a function of their height, a feat that would be taxing to a modern physicist using calculus.

Apart from general physics he was an astronomer, and Cicero writes that in the year 212 BC when Syracuse, Italy was raided by Roman troops, the Roman consul Marcellus brought a device which mapped the sky on a sphere and another device that predicted the motions of the sun and the moon and the planets (i.e. a planetarium) to Rome. He credits Thales and Eudoxus for constructing these devices. For some time this was assumed to be a legend of doubtful nature, but the discovery of the Antikythera mechanism has changed the view of this issue, and it is indeed probable that Archimedes possessed and constructed such devices. Pappus of Alexandria writes that Archimedes had written a practical book on the construction of such spheres entitled On Sphere-Making.

Archimedes' works were not very influential, even in antiquity. He and his contemporaries probably constitute the peak of Greek mathematical rigour. During the Middle Ages the mathematicians who could understand Archimedes' work were few and far between. Many of his works were lost when the library of Alexandria was destroyed and survived only in Latin or Arabic translations. As a result, his mechanical method was lost until around 1900, after the arithmetization of analysis had been carried out successfully. We can only speculate about the effect that the "method" would have had on the development of calculus had it been known in the 16th and 17th centuries.

ARCHIMEDES SCREW

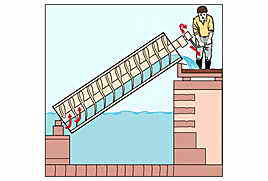
he Archimedes screw, a spiral screw turned inside a cylinder, was once commonly used to lift water from canals. The screw is still used to lift water in the Nile delta in Egypt, and is often used to shift grain in mills and powders in factories.
(Image © Research Machines plc)

One of the earliest kinds of pump, associated with the Greek mathematician Archimedes. It consists of an enormous spiral screw revolving inside a close-fitting cylinder. It is used, for example, to raise water for irrigation.

Archimedes Screw

The lowest portion of the screw just dips into the water, and as the cylinder is turned a small quantity of water is scooped up. The inclination of the cylinder is such that at the next revolution the water is raised above the next thread, whilst the lowest thread scoops up another quantity. The successive revolutions, therefore, raise the water thread by thread until it emerges at the top of the cylinder.

The Law of the Lever Before Archimedes

Why is it that small forces can move great weights by means of a lever, as was said at the beginning of the treatise, seeing that one naturally adds the weight of the lever? For surely the smaller weight is easier to move, and it is smaller without the lever. Is the lever the reason, being equivalent to a beam with a cord attached below, and divided into two equal parts? 

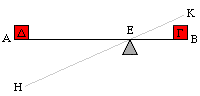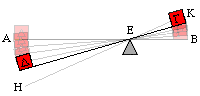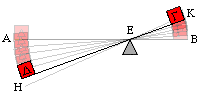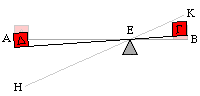
For the fulcrum acts as the attached cord : for both these remain stationary, and act as a centre. For since under the impulse of the same weight the greater radius from the centre moves the more rapidly, and there are three elements in the lever, the fulcrum,that is the cord or centre, and the two weights, the one which causes the movement, and the one that is moved : now the ratio of the weight moved to the weight moving it is the inverse ratio of the distances from the centre.

 Now the greater the distance from the fulcrum, the more easily it will move. The reason has been given before that the point further from the centre describes the greater circle, so that by the use of the same force, when the motive force is farther from the lever, it will cause a greater movement. Let AB be the bar, G be the weight, and D the moving force, E the fulcrum ; and let H be the point to which the moving force travels and K the point to which G the weight moved travels.

Writings by Archimedes

• On the Equilibrium of Planes (2 volumes)

This book spells out the law of the lever and uses it to calculate the areas and centers of gravity of various geometric figures.

• On Spirals

In this book, Archimedes defines what is now called Archimedes' spiral. This is the first mechanical curve (i.e., traced by a moving point) ever considered by a Greek mathematician. Using this curve, he was able to square the circle.

• On the Sphere and The Cylinder

In this book Archimedes obtains the result he was most proud of: that the area and volume of a sphere are in the same relationship to the area and volume of the circumscribed straight cylinder.

• On Conoids and Spheroids

In this book Archimedes calculates the areas and volumes of sectios of cones, spheres and paraboloids.

• On Floating Bodies (2 volumes)

In the first part of this book, Archimedes spells out the law of equilibrium of fluids, and proves that water around a center of gravity will adopt a spherical form. This is probably an attempt at explaining the observation made by Greek astronomers that the Earth is round. Note that his fluids are not self-gravitating: he assumes the existence of a point towards all things fall and derives the spherical shape. One is led to wonder what he would have done had he struck upon the idea of universal gravitation.

 

In the second part, a veritable tour-de-force, he calculates the equilibrium positions of sections of paraboloids. This was probably an idealization of the shapes of ships' hulls. Some of his sections float with the base under water and the summit above water, which is reminiscent of the way icebergs float, although Archimedes probably wasn't thinking of this application.

• The Quadrature of the Parabola

In this book, Archimedes calculates the area of a segment of a parabola (the figure delimited by a parabola and a secant line not necessarily perpendicular to the axis). The final answer is obtained by triangulating the area and summing the geometric series with ratio 1/4.

• Stomachion

This is a Greek puzzle similar to Tangram. In this book, Archimedes calculates the areas of the various pieces. This may be the first reference we have to this game. Recent discoveries indicate that Archimedes was attempting to determine how many ways the strips of paper could be assembled into the shape of a square. This is possibly the first use of combinatorics to solve a problem.

• Archimedes' Cattle Problem

Archimedes wrote a letter to the scholars in the Library of Alexandria, who apparently had downplayed the importance of Archimedes' works. In these letters, he dares them to count the numbers cattle in the Herd of the Sun by solving a number of simultaneous diophantine equations, some of them quadratic. This problem is one of the famous problems solved with the aid of a computer.

• The Sand Reckoner

In this book, Archimedes counts the number of grains of sand fitting inside the universe. This book mentions Aristarchus' theory of the solar system, contemporary ideas about the size of the Earth and the distance between various celestial bodies. From the inroductory letter we also learn that Archimedes' father was an astronomer.

• "The Method"

In this work, which was unknown in the Middle Ages, but the importance of which was realised after its discovery, Archimedes pioneered the use of infinitesimals, showing how breaking up a figure in an infinite number of infinitely small parts could be used to determine its area or volume. Archimedes did probably consider these methods not mathematically precise, and he used these methods to find at least some of the areas or volumes he sought, and then used the more traditional method of exhaustion? to prove them. This particular work is found in what is called the Archimedes Palimpsest. Some details can be found at how Archimedes used infinitesimals.

 

Quotes about Archimedes

• "Perhaps the best indication of what Archimedes truly loved most is his request that his tombstone include a cylinder circumscribing a sphere, accompanied by the inscription of his amazing theorem that the sphere is exactly two-thirds of the circumscribing cylinder in both surface area and volume!" (Laubenbacher and Pengelley, p. 95)

• "...but regarding the work of an engineer and every art that ministers the needs of life as ignoble and vulgar, he devoted his earnest efforts only to those studies the subtlety and charm of which are not affected by the claims of necessity." Plutarch, possibly explaining why Archimedes produced no writings that describe precisely the design of his inventions.

Named after Archimedes

• Archimedes crater on the Moon.

• Asteroid 3600 Archimedes, named in his honour

• Archimedes computer

• Archimedean tilings, Archimedean spirals, Archimedean solids, Trammal of Archimedes.

LINKS :

• Archimedes and the Rhombicuboctahedron (http://agutie.homestead.com/files/rhombicubocta.html) by Antonio Gutierrez from Geometry Step by Step from the Land of the Incas.

• Archimedes Home Page (http://www.mcs.drexel.edu/~crorres/Archimedes/contents.html)

• MacTutor biography of Archimedes (http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Archimedes.html)

• The Archimedes Palimpsest (http://www.thewalters.org/archimedes/frame.html) web pages at the Walters Art Museum.

• Archimedes - The Golden Crown (http://www.mcs.drexel.edu/~crorres/Archimedes/Crown/CrownIntro.html) points out that in reality Archimedes may well have used a more subtle method than the one in the classic version of the story.

• Archimedes' Quadrature Of The Parabola (http://www.math.ubc.ca/~cass/archimedes/parabola.html) Translated by Thomas Heath.

• Archimedes' On The Measurement Of The Circle (http://www.math.ubc.ca/~cass/archimedes/circle.html) Translated by Thomas Heath.

• Archimedes' Cattle Problem (http://www.mcs.drexel.edu/~crorres/Archimedes/Cattle/Statement.html)

• eTexts (http://www.gutenberg.net/catalog/world/authrec?fk_authors=2545) of Archimedes' works, at Project Gutenberg

• Angle Trisection by Archimedes of Syracuse (Java) (http://www.cut-the-knot.org/pythagoras/archi.shtml)

• Archimedes'Triangle (Java) (http://www.cut-the-knot.org/ctk/Parabola.shtml#ArchimedesTriangle)

• An ancient extra-geometric proof (http://www.cut-the-knot.org/pythagoras/Archimedes.shtml)

• Archimedes' Squaring of Parabola (Java) (http://www.cut-the-knot.org/ctk/Parabola.shtml#SqParabola)

INVENTORS A - Z

The ultimate Robot Boat. Solarnavigator uses an advanced SWASSH hull as the platform 

to mount the world's first autonomous circumnavigation. A successful expedition could pave the way for improved safety at sea.

This website is copyright © 1991- 2013 Electrick Publications. All rights reserved. The bird logo and names Solar Navigator and Blueplanet Ecostar are trademarks ™.  The Blueplanet vehicle configuration is registered ®.  All other trademarks hereby acknowledged and please note that this project should not be confused with the Australian: 'World Solar Challenge'™which is a superb road vehicle endurance race from Darwin to Adelaide.  Max Energy Limited is an educational charity working hard to promote world peace.

 AUTOMOTIVE  |  BLUEPLANET BE3  |  ELECTRIC CARS  |  ELECTRIC CYCLES  |  SOLAR CARS  |  SOLARNAVIGATOR