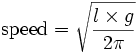|
|
||
|
Wave making resistance is a form of drag that effects surface Watercraft, such as boats and ships, and reflects the energy required to push the water out of the way of the hull. This energy goes into creating the wake.
Graph of wave-making resistance of a displacement hull, with a mark at a speed/length ratio of 1.34
Physics
For small displacement hulls, such as sailboats or rowboats, wave making resistance is the major source of drag. The unique properties of deepwater waves (where the water depth is deeper than the half the wavelength) mean that the wave making resistance is very dependent upon the hull's interaction with the wake.
The propagation speed of deepwater waves is proportional to the square root of the wavelength of the generated waves, and the wavelength of a boat's wake is based on its waterline length — so: there is a direct relationship between the waterline length (and thus wave propagation speed) and the rate at which drag increases.
A simple way of considering wave-making resistance is to look at the hull in relation to its wake. At speeds lower than the wave propagation speed, the wave rapidly dissipates to the sides. As the hull approaches the wave propagation speed, however, the wake at the bow begins to build up faster than it can dissipate, and so it grows in amplitude. Since the water is not able to "get out of the way of the hull fast enough", the hull, in essence, has to climb over or push through the bow wave. This results in an exponential increase in resistance with increasing speed.
To calculate the speed of wave propagation, the following formula is used:
Plugging in the appropriate value for gravity and solving yields the equation:
Or, in metric units:
These values, 1.34 and 2.5, are often used in the hull speed rule of thumb used to compare potential speeds of displacement hulls, and this relationship is also fundamental to the Froude number, used in the comparison of different scales of watercraft.
When the vessel exceeds a speed/length ratio of 0.94, it starts to outrun most of its bow wave, the hull actually settles slightly in the water as it is now only supported by two wave peaks. As the vessel exceeds a speed/length ratio of 1.34, the hull speed, the wavelength is now longer than the hull, and the stern is no longer supported by the wake, causing the stern to squat, and the bow rise. The hull is now starting to climb its own bow wave, and resistance begins to increase at a very high rate. While it is possible to drive a displacement hull faster than a speed/length ratio of 1.34, it is prohibitively expensive to do so. Most large vessels operate at speed/length ratios well below that level, at speed/length ratios of under 1.0.
Ways of reducing wave making resistance
Since wave making resistance is based on the energy required to push the water out of the way of the hull, there are a number of ways that this can be minimized.
Reduced displacement
Reducing the displacement of the craft, by eliminating excess weight, is the most straightforward way to reduce the wave making drag. Another way is to shape the hull so as to generate lift as it moves through the water. Semi-displacement hulls and planing hulls do this, and they are able to break through the hull speed barrier and transition into a realm where drag increases at a much lower rate. The downside of this is that planing is only practical on smaller vessels, with high power to weight ratios, such as motorboats. It is not a practical solution for a large vessel such as a supertanker.
Fine entry
A hull with a blunt bow has to push the water away very quickly to pass through, and this high acceleration requires large amounts of energy. By using a fine bow, with a sharper angle that pushes the water out of the way more gradually, the amount of energy required to displace the water will be less, even though the same total amount of water will be displaced. A modern variation is the wave-piercing design.
Bulbous bow
A special type of bow, called a bulbous bow, is often used on large motor vessels to reduce wave making drag. The bulb alters the waves generated by the hull, but due to its very limited range of effect, is only useful on large motor vessels operating at constant speeds.
Semi-displacement and planing hulls
A graph showing resistance/weight ratio as a function of speed/length ratio for displacement, semi-displacement, and planing hulls.
Since semi-displacement and planing hulls generate a significant amount of lift in operation, they are capable of breaking the barrier of the wave propagation speed and operating in realms of much lower drag, but to do this they must be capable of first pushing past that speed, which requires significant power. Once the hull gets over the hump of the bow wave, the rate of increase of the wave drag will start to reduce significantly.
Wave Piercing Hulls
A wave-piercing boat hull has a very fine bow, with reduced buoyancy in the forward portions.
When a wave is encountered, the lack of buoyancy means the hull pierces through the water rather than riding over the top - resulting in a smoother ride than traditional designs, and in diminished stress on the vessel and crew. It also reduces a boat's wave making resistance.
Design theory calls for very long thin hulls, so in practice most are multi-hulls such as catamarans.
The main current usage areas are passenger ferries and military craft.
LINKS and REFERENCE
|
||
|
This
website
is Copyright © 1999 & 2007 Electrick Publications.
The bird The name '1824' is a trade mark of Solar Cola Ltd. All rights reserved. Max Energy Limited is an educational charity.
|